Most people are familiar with the concept of going to the bank and getting a loan to buy a house, but how many of us know how 30 year mortgages get paid off? Is it similar to a car loan where most of the payment goes toward paying off the principal balance and the rest toward the interest? Do these portions stay the same or do they change with time?
Most people would be surprised to learn that the very first mortgage payment they make is mostly interest. This is a lot different from a typical car loan payment.
What is Amortization?
Amortization is the paying down of debt over time.
The most common type of amortization is referred to as straight-line amortization, or a level payment amortized loan. In straight-line amortization, payments are made in equal installments until the loan is completely paid back, or amortized. Since the payment amount is always greater than the interest owed, each payment is broken down and applied first to the interest owed, then the rest is paid to the principle amount.
The total payment each month will stay the same, but the amount paid towards interest will decrease, while the amount paid towards the principal will increase.
For example, if you borrow $200,000, at 4% interest, with a 30 year amortization schedule, your principal & interest payment will be $955 per month.
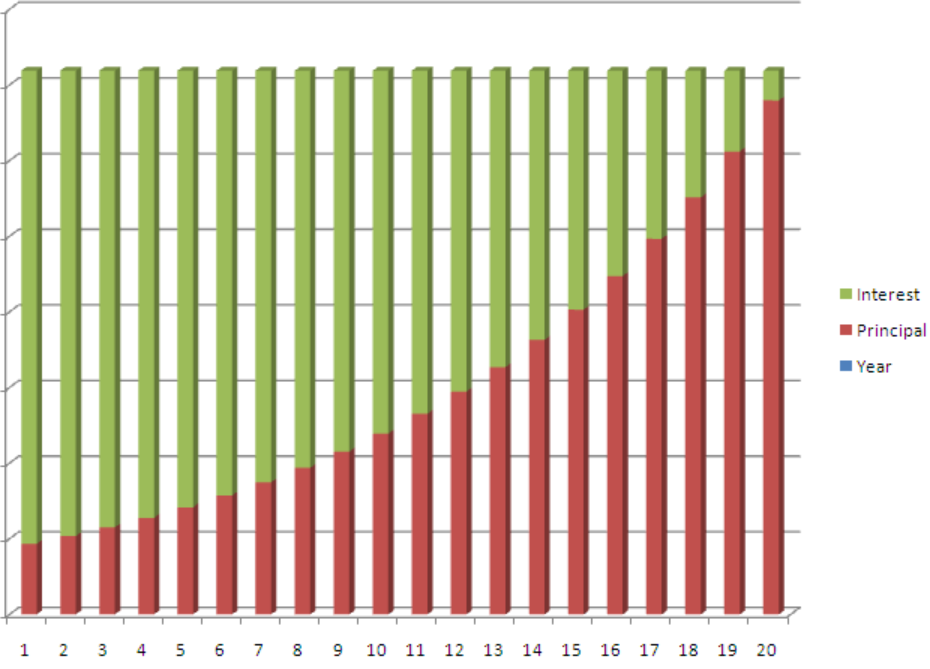
If you look at the graph above, there are 20 bars each representing 1 year of principle and interest payments for this plan. The amount of the interest payment is filled in green, and the principal payment is filled in red.
The payment remains the same throughout the life of the loan. However, the amount of the payment that is allocated to the interest is filled in green. Can you see how early in the loan most of the payment goes to the interest?
During the early years, the interest amount is largest because the principle loan amount hasn’t been paid back as much yet. Each payment reduces the amount of principle, so the next payment will not accrue as much interest. The combined area of the white space will add up to the total principle once the loan is amortized.
As the years go on the principle will continue to get smaller, which will lead to less interest so more money of each payment will be applied to paying the principle.
Let’s Look at an Example
In this example, a home has been purchased for $135,000, with $13,500 down, and $121,000 has been borrowed at 3.5% interest. The amortization schedule is for 30 years.
$135,000 – Purchase Price
3.5% – Rate
$13,500 – Down Payment
$121,000 – Loan Amount
| PMT NO. | Int Rate | Balance | Payment | Interest | Principle |
|---|---|---|---|---|---|
| 1 | 3.50% | $121,308 | $545.59 | $354.38 | $191.21 |

I’ve taken an excerpt from the amortization schedule, shown above, and we see that the first payment on the property is a total of $545.59 (I’ve excluded the taxes and insurance portion to keep things simple).
Now, what I want to emphasis is that $354.28 went toward the interest and only $191.21 went to the principal balance. In the early part of the loan most of the payment goes toward the interest. As time goes on, this ratio of principle to interest will begin to move toward paying the principle.

Let’s take a look at the chart at year 5:
| PMT NO. | Int Rate | Balance | Payment | Interest | Principle | Cumulative Interest | Cumulative Principle | |
|---|---|---|---|---|---|---|---|---|
| 60 | 3.50% | $109,209.01 | $545.59 | $318.53 | $227.06 | $20,217.30 | $12,518.06 |

The 1st payment of the 5th year will be the 60th payment (see above). The mortgage payment has remained the same except $227.06 is now being applied to the principal balance.
Notice how the principal amount of the loan has been reduced to $109,209.01 over a period of 5 years.
Note, the last column on the right labeled “Cumulative Principle”, $12,518.06 is the total amount of the principle balance that has been paid back. So, as time goes on, you continue to pay down the loan and create what is referred to as “equity in the home”.
Now lets look at the first payment at the 10th year (payment no. 120) below:
| PMT NO. | Int Rate | Beginning Balance | Payment | Interest | Principle | Cumulative Interest | Cumulative Principle | |
|---|---|---|---|---|---|---|---|---|
| 120 | 3.50% | $94,344.07 | $545.59 | $275.17 | $270.42 | $38,044.37 | $27,426.35 |
The amount of money being applied to the principal and interest is now about equal: $275.17 going to the interest and $270.42 going to the principle. In this example $27,426.35 has been paid back (see the final column on the right labeled “Cumulative Principle”.
What do you think would happen if we changed the interest rate? What if we kept the same purchase price, down payment, and loan amount, but increased the interest rate to 5%.

An Increase in Interest Rate
$135,000 – Purchase Price
5% – Interest Rate
$13,500 – Down Payment
$121,500 – Loan Amount
| PMT NO. | Int Rate | Payment | Interest | Principle | Balance | Cumulative Interest | Accumulative Principle | |
|---|---|---|---|---|---|---|---|---|
| 1 | 5% | $545.59 | $506.25 | $145.99 | $121,354.01 | $506.25 | $145.99 |
You can now see that only $145.99 is being applied to the principle with the interest rate being 5%. This is only a $45 difference from our first example with a 3.5% interest rate. This doesn’t seem like much, but let’s look further down the road.
Take a look at the 10th year and compare that to our first example:
| PMT NO. | Interest Rate | Beginning Balance | Payment | Interest | Principle | Balance | Cumulative Interest | Accumulated Principle |
|---|---|---|---|---|---|---|---|---|
| 120 | 5% | $98,830.61 | $545.59 | $412.79 | $239.45 | $98,830.61 | $55,599.20 | $22,699.39 |
Now look at the difference between the interest payment of $412.79 and the principal payment of $239.45
Now compare that with our initial example where the interest rate was lower and the payments were about equal in the 10th year.
| PMT NO. | Interest Rate | Interest | Principle |
|---|---|---|---|
| 120 | 3.50% | $275.17 | $270.42 |

Higher interest rate loans are far more expensive than one might think. The amount of interest being paid on a mortgage has a significant impact on the speed at which you build equity in the property.
For example:
If 2 people took out 30 year fixed mortgages for $121,000 each, but 1 person was paying 3.5% interest and the other was paying 5%, we can compare the balance that each would have to pay back by year 10.
| Mortgage A. | Mortgage B. | ||||
|---|---|---|---|---|---|
| PMT NO. | Interest Rate | Principle Balance | PMT No. | Interest Rate | Principle Balance |
| 120 | 3.50% | $94,344.07 | 120 | 5% | $98,830.61 |
A difference of $4,486.54!
This is an important concept to understand before you decide to refinance. Homeowners that refinance multiple-times will keep returning to the interest-paying portion of the loan.
What are the advantages of getting a mortgage?
Affordability
A 30 year mortgage makes the monthly payments, and hence the home, more affordable to a greater number of people. It’s worth nothing that at the beginning of the 20th century only 46% of Americans owned a home. That number had piqued to about 69% in the mid-2000’s and has declined to about 65% since then. It’s true that down payment requirements had a major impact but we will not get into that here.
It’s also more efficient than saving up for an all cash purchase. If you were to rent a home for an extended period of time, your rent would continue to increase, you would receive no tax deduction from your mortgage interest, and you would have no equity.
One feature of all mortgages is that you are free to add extra money to your mortgage payment that can only be applied to your principle, thereby shortening the term of the loan.
Also, you have the option of obtaining shorter amortization periods, anywhere from 15 – 30 years. Many of the 15 year amortized loan come with lower interest rates than their 30 year counterparts.